|
|
||
|---|---|---|
| fig | ||
| sounds | ||
| .gitignore | ||
| README.md | ||
| fft-decode.py | ||
| fft-graph.py | ||
| generate.py | ||
| soundbox.py | ||
| stft-decode.py | ||
| stft-graph.py | ||
README.md
À la recherche des notes originelles
À partir de l’enregistrement numérique d’une interprétation musicale, est-il possible de reconnaître la séquence de notes qui a été jouée sur les différents instruments utilisés ? Cette situation s’apparente à celle où l’on dispose d’une image matricielle rendue à partir d’une image vectorielle et où l’on souhaite retrouver les vecteurs d’origine dont on ne dispose plus — à la différence que nous traitons ici d’un signal 1D au lieu de 2D, et d’un signal sonore plutôt que visuel qui plus est.
Excursion sinusoïdale
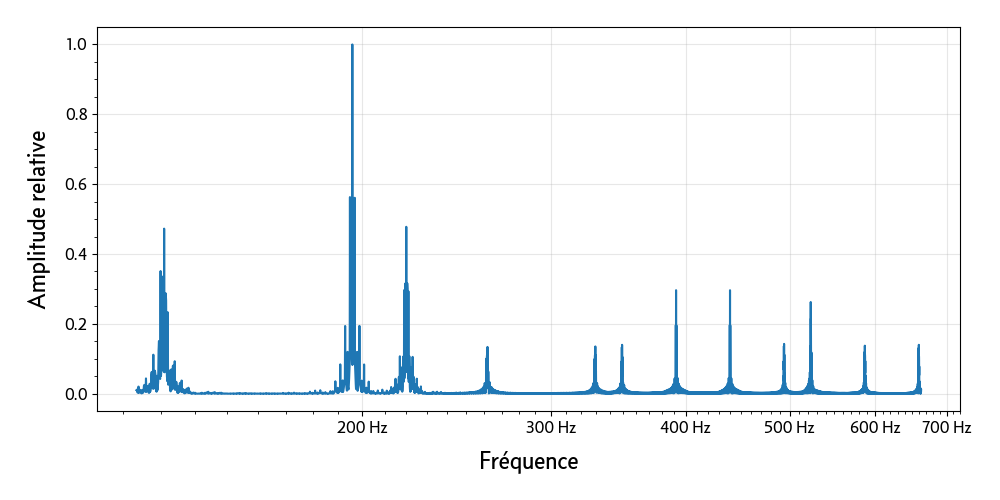
Simplifions d’abord le problème en considérant un signal composé uniquement de sinusoïdes pures (produit par le synthétiseur de fortune qu’est ce script Python). Cela facilite doublement la tâche, puisque non seulement le signal est totalement exempt de bruit, mais en plus les instruments convoqués n’ont qu’une seule harmonique. Une première approche consiste à étudier le spectre du signal en utilisant une transformation de Fourier (générée par ce script Python).
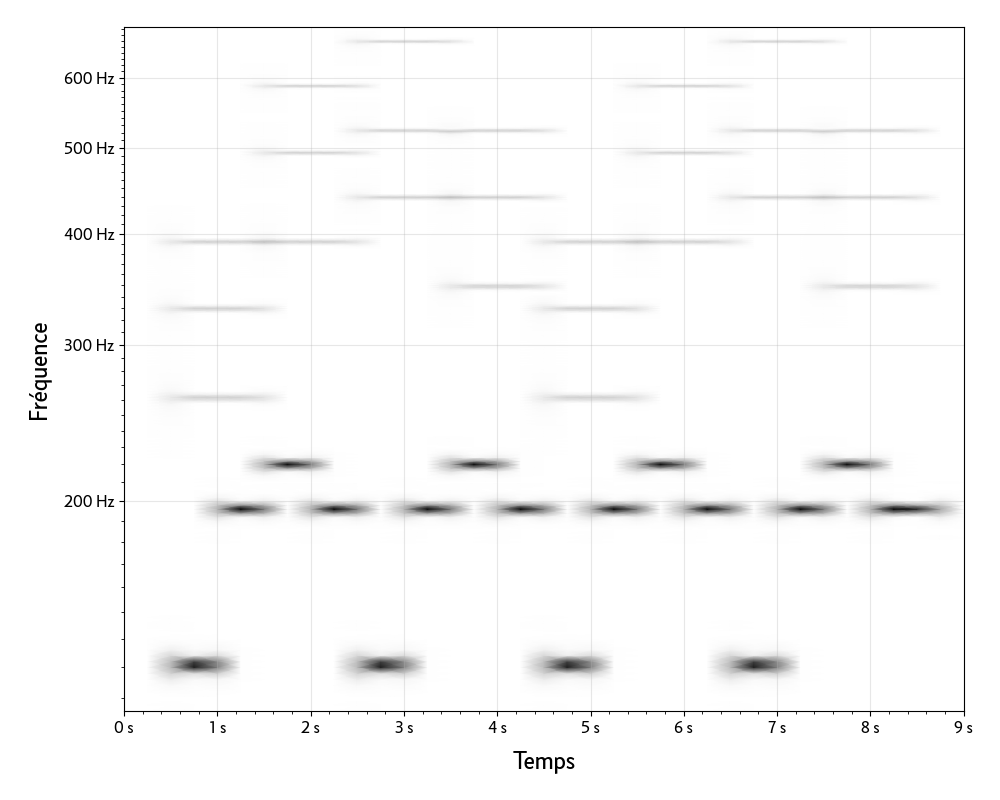
Sur ce spectre peuvent être distinguées les douze notes qui composent le morceau : do₂, sol₂, la₂, do₃, mi₃, fa₃, sol₃, la₃, si₃, do₄, re₄, mi₄. Une information cruciale manque cependant, celle de l’évolution du signal dans le temps. Une façon de l’obtenir consiste à découper le signal en courtes fenêtres de temps et d’appliquer la transformation de Fourier sur les segments obtenus : c’est la transformée de Fourier à court terme. On obtient ainsi un sonagramme qui montre l’évolution des fréquences du signal dans le temps (produit par ce script Python).
Ce sonagramme permet de distinguer clairement les deux parties du morceau, celle jouée par une sinusoïde au dessus de 250 Hz et celle jouée par une onde carrée en dessous de cette fréquence. On reconnaît également les quatre accords en do majeur joués par la sinusoïde deux fois de suite. Sur cet exemple simple, la transformée de Fourier à court terme est donc suffisante pour extraire les notes, mais qu’en est-il d’un signal plus complexe ?